An old take-down of a silly TED talk

Originally published in June, 2015.

Sorry, I don’t have a musicology blog, so this will have to do.

I occasionally get roped into discussions when my friends find some bit of internet detritus that has some musicological bearing. Before yesterday, it was the horseshit known as “432 tuning,” which will apparently open your mind and make all of your music sound the way god intended it, or some such thing. The latest installment is a TEDx talk from 2011 by some guy named Scott Rickard who seems to know more about mathematics than music, but it’s really hard to tell. I can only guess that mathematicians roll there eyes with equal ferocity when composers try to expound on mathematical topics—something that happens far too frequently—but Jesus Christ, this talk is a mess. Let’s get right to it, shall we?

“Most musicologists would argue…”

Yes. Yes they would. Rickard starts his talk by asking a question that does not bode well for the rest of the talk: “What makes a piece of music beautiful?” In fact, it was at this point when this video was first posted, that I turned it off and replied to the post, “Can I give a TED talk where I just punch this guy in the face over and over.” But then another musicologist friend posted it with the provocative tag-line “too many problematic statements to enumerate here,” and I decided maybe it would be worth seeing exactly how bad it gets. Rickard immediately answers his question with the assertion that “Most musicologists would argue that repetition is a key aspect of beauty.” The simplest refutation to that statement is to say, no, musicologists do not agree. But if he had bothered to speak with a musicologist, he might have been surprised to know that we do not customarily spend our time trying to answer these sorts of questions. This is mostly because, as his talk so aptly shows, no good will come of it. Had he decided to make a TED talk coming to some conclusion about what makes music beautiful, maybe starting with a summary of Hanslick, that would have been bad enough. Instead, he just tells his audience that musicologists all know what makes music beautiful, and guess what? It’s repetition! Whew, glad we cleared that up.

“What would it sound like if we wrote a piece of music that had no repetition in it whatsoever?”

Umm. Ok. Sure, I guess this is not a trivial thing, and he gets to tell his audience some mathematical things that are I think supposed to convince us that he knows what he’s talking about. The main point of this section seems to be that random is not the same as pattern free. So if we play random notes on a piano, it’s not going to be as ugly as making something that has no pattern whatsoever. (Because, beauty and ugliness is exclusively a factor of how much repetition a piece contains, remember?) He goes on to talk about sonar and pings and hhhhhhhhhhhhhhhhhhhhhhhhhhh….oh, sorry, I just fell asleep with my hand on the keyboard. So to summarize, some famous mathematicians had to deal with making a non-patterning series of numbers to make sonar work properly. And for some reason he thinks its important to tell us about how Évariste Galois died in a duel in the process. He decides to show us a pattern-free array of the numbers between 1 and 88 because that’s how many notes there are on a piano.

“So today, we’re going to have the world premiere of the world’s first pattern-free piano sonata”

Ok, let’s just ignore the fact that a “piano sonata” is a form based on repetitions of themes and sections. Rickard wouldn’t be the first to break that particular rule, and I’m sure he won’t be the last.

“So back to the question of music, so, what makes music beautiful?”

Wait, I thought we covered this? Oh, I get it, we need some empirical scientific evidence to support our claim that repetition is what makes music beautiful. What is empirically and scientifically the most beautiful piece of music ever written?? Beethoven’s Fifth, of course. I guess I’m glad to see that scientists have no more idea how to apply scientific rigor to musical analysis than music theorists, I suppose. Let’s just go ahead and pretend that Beethoven 5 is the most beautiful piece of music ever written, and not, say, “Soave sia il vento.” That clearly means that, because the “fate knocking at the door” theme is repeated so much, that must be why it is the most beautiful. There’s clearly no other explanation. Why Beethoven didn’t figure out how to make his subsequent symphonies more repetitive instead of writing such ugly drivel like the Seventh is one of the great questions for musicology.

Ok, so Beethoven 5 is the most beautiful piece ever. Let’s make a continuum from there to the most ugly possible piece of music ever written or conceived. “Random music,” maybe Cage’s Music of Changes, is on that continuum, pretty far from Beethoven. It is pretty fucking ugly, after all. But according to our mathematical scheme, random is not the same as pattern free; we can make something much more ugly than Music of Changes. If you’re looking for a kernel of something in this talk that is not completely stupid, this is it. Yes. there is a difference between random music and the avoidance of patterns. Cage knew this very well, as does any musicologist or composer who works on later-20th century aleatoric music. The goal of chance music was very rarely the avoidance of patterns. But to suggest that this has anything to do with a quantifiable sense of “how beautiful a piece of music is”? Ugh.

“It turns out musicologists, a famous composer by the name of Arnold Schoenberg…”

This is the point in the talk when you need to be sure you don’t have any sharp implements at hand or you may find yourself trying to insert them into your eye-holes. He goes on to say that Schoenberg “thought of this in the 1930s, 40s, and 50s.” I guess I can’t say for certain that Schoenberg never though about this in the “1930s, 40s, and 50s” though I’m guessing he probably didn’t think about it very often in the 50s given that he died in 1951. I’m not a mind reader, after all. I think about all sorts of stupid things on any given day, so who knows. He goes on, “His goal as a composer was to write music that would free music from tonal structure. He called it the emancipation of the dissonance.” Sure, I guess. Given what Rickard has said so far, I’m not going to quibble that one. He goes on to say that Schoenberg created these structures called “tone rows, that sound a lot like a ‘Costas Array.’” He points to one in his powerpoint slide. He fails to mention that those tone rows are repeated over and over, and that the goal Schoenberg had in mind was to create thematic unity, i.e. repetition, not the avoidance of patterns. In terms of Schoenberg’s “motivation,” the goal was probably closer to taking Beethoven 5 and letting it smoke crack. So Schoenberg’s 12-tone pieces are actually the most beautiful pieces ever written. Nice to clear that up. He goes on, “Unfortunatley [Schoenberg] died 10 years before Costas solved the problem of how you can mathematically create these structures.” Poor Schoenberg. If only he had lived, he could have realized his dream of writing music completely devoid of patterns, since we all know Schoenberg’s goal was to write the ugliest piece of music ever. Oh, for fuck’s sake. Thank god it’s over at this point, and he goes on to actually have someone play his piece.

The piece, by the way, is exactly what you’d expect from a mathematician who has decided to write the ugliest piece of music he can imagine. It’s not so much ugly as dumb. And, oh yeah, it totally fails to do what he says it will, because he’s never heard of the idea of pitch class. And because he thinks we hear music in the same way we read a mathematical chart. I mean, Jesus, do I really have to explain this shit. OK, it seems like I do. The pitch class issues mean that while he’s cycling through the 88 notes of the piano as if they are all equally discrete things, there are actually only 12 different pitch classes. So while there may be no pattern to the distribution of the 88 discrete notes, there will almost certainly be unintended patterns to the repetition of pitch classes. Here, for example are the first 12 notes of his piece (I wrote a little php program to generate the piece here.)

1 – A
3 – B
9 – F
27 – B
81 – F
65 – C-Sharp
17 – C-Sharp
51 – B
64 – C
14 – A-Sharp
42 – D
37 – A

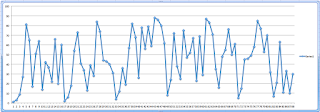
You can already see a nice B-F-B-F pattern followed by an octave leap on the C-Sharp, before returning to another B. There’s lots of that kind of thing in the piece. He at least tried to deal with rhythm by using a “Golomb ruler so that the starting time for each pair of notes is distinct as well.” I think he meant to say that the spacing between each note is different, since just playing all the notes in succession will make sure that no two notes are played at the same time. But this slip isn’t just a problem of clarity. He’s just revealed that he has no idea how music works. For one thing, he ignored the entire problem of harmony. No notes happen simultaneously, and the reason seems to be that he just didn’t think about it. Sure the spacing is inconsistent, but it is completely linear. To believe that listeners will not hear patterns (“revel in the fact that you won’t find any,” he says) ignores the way that humans listen to music. Ignoring the previously mentioned pitch class issues, we do not recognize patterns solely in terms of pitch repetitions. In an atonal context such as this, one typically recognizes contours before pitch. And the contours of this piece are actually quite predictable because of the way that the pitches were generated. The piece is really just a very simplistic algorthmic composition. To describe the algorithm quickly, you start at the bottom note (starting at the bottom also creates a certain teleology…but I digress) (oh, and sorry, another digression, there is also a clear teleology to the idea that the performer is playing all 88 notes in succession), you multiply that number (1) by three to pick the next note. You keep doing that until you get a note above the upper limit of 88. You then subtract 89 until you get back to a note below 88, in this case 65, and start over. The next note is 195, again above the 88 limit, so subtracting 89 twice gets you back to 17, followed by 51, and so on. This creates a pattern to the contour of the piece. Any note below 29 (C-sharp 3) will be followed by a higher note. Notes above that threshold might go up or down, but the generating principle causes there to be a rising trajectory through most of the gestures. And for god’s sake, there’s almost a step progression up to the highest note (88, high C). Here, look for yourself.